Verschlüsselung mit elliptischen Kurven

Im Kreis

Jan Bundesmann

Mit immer mehr Rechenleistung versuchen Angreifer, verschlüsselte Botschaften zu knacken. Die Reaktion: längere Schlüssel. Damit Smartphones und Smartcard dabei nicht in die Knie gehen, greift man auf elliptische Kurven zurück.

Gängige Verschlüsselungsverfahren nutzen Funktionen, die in eine Richtung schnell auszuführen sind, deren Umkehrung jedoch deutlich mehr Rechenleistung erfordert: Trap-Door-Funktionen. Man spricht von mathematischer Sicherheit, denn sie beruht auf der Entschlüsselungszeit. Das schließt nicht aus, dass in Zukunft ein Verfahren als unsicher betrachtet werden muss, weil neuere Computer mehr Leistung besitzen. Eine Trap-Door-Funktion ergibt sich aus dem diskreten Logarithmusproblem, auf dem letztlich auch die Verschlüsselung mit elliptischen Kurven aufbaut.

Als Maß für die Sicherheit eines Verfahrens gilt die Zahl der nötigen Schritte, um es mit dem besten Verfahren zu knacken. Handelt es sich dabei etwa um 2⁸⁰ nötige Schritte, spricht man von einem Sicherheitsniveau von 80 Bit. Zum Vergleich: Verschlüsseln mit elliptischen Kurven und 160 Bit langem Schlüssel entspricht RSA- oder DSA-Verschlüsselung mit 1024 Bit. Dieser Wert ist eine untere Grenze, denn gerade großen Nachrichtendiensten wird nachgesagt, die nötige Rechenleistung zum schnellen Entschlüsseln derartiger Chiffren bereits im Einsatz zu haben. Auf längere Sicht empfiehlt sich ein höheres Sicherheitsniveau. Setzt man dafür 128 Bit an, sollten herkömmliche Verfahren Schlüssel mit 3072 Bit verwenden, bei elliptischen Kurven reichen 256 Bit.

Geheimer Schlüsseltausch

Der gewöhnliche Logarithmus als Umkehrung von Exponentialfunktionen lässt sich relativ schnell berechnen. Komplizierter ist der diskrete Logarithmus in endlichen Zahlenräumen. Ein typisches Beispiel ist der Restklassenring modulo 11. Dieser besteht aus den ganzen Zahlen von 0 bis 10. Um damit praktisch zu rechnen, bildet man alle Zahlen auf ihren Rest bei der Teilung durch 11 ab. Die 17 entspräche dann etwa der 6, die 23 wird zur 1.

Zwei Partner, die kommunizieren wollen – wie in der Kryptografie-Literatur üblich Alice und Bob –, könnten sich auf folgendes Setup verständigen: Restklassenring modulo 11, 9 als sogenannter Generator. Nun wählen die beiden Zahlen x und y zwischen 1 und 10 als ihre geheimen Schlüssel (Private Keys). An die Partner übermitteln sie ihre öffentlichen Schlüssel 9^x beziehungsweise 9^y. Alice übermittelt an Bob beispielsweise 5 und erhält von ihm im Tausch seinen Public Key 4. Letzteren kann sie wiederum mit ihrem geheimen Schlüssel potenzieren, um das gemeinsame Geheimnis 3 zu erfahren. Ebenso verfährt Bob und erfährt aufgrund der Vertauschbarkeit bei der Multiplikation denselben Wert. Fertig ist der Diffie-Hellman-Schlüsselaustausch.

Anhand dieser Zahlen lässt sich die Stärke des Verfahrens nicht erkennen – sogar von Hand errechnen Angreifer Alices und Bobs private Schlüssel 4 und 7 in wenigen Schritten. Mit etwas Glück hat man sogar schon eine Tabelle für dieses Setup vorberechnet. Bei größeren Schlüsseln scheitern Kryptoanalyseverfahren allerdings an der dafür nötigen Rechenzeit oder am benötigten Speicher.

Anstelle des Rings aus ganzen Zahlen lassen sich andere zyklische Gruppen konstruieren. Elliptische Kurven bestehen aus Punktmengen, deren Koordinaten auf einer „Kurve“ liegen. In zwei Dimensionen lautet eine mögliche Kurvengleichung etwa

y² ≡ x³  + a x + b mod p

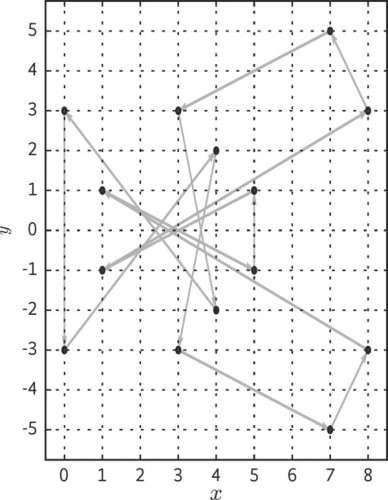
Die Elemente der elliptischen Kurve x² ≡ y³ + 2 x + 2 mod 11. Nimmt man als Generator den Punkt (5,1), erhält man durch sukzessives Addieren alle weiteren Punkte (graue Pfeile).

Zwei Punkte können „addiert“ werden, wofür spezielle Vorschriften existieren, damit das Ergebnis auf der Kurve liegt. Ebenfalls gibt es „Generatoren“: Punkte, deren wiederholte Addition {1×P, 2×P, 3×P, …} alle Punkte der Menge abdeckt (siehe Abbildung). Genau wie im vorherigen Beispiel kann ein Dritter die Rechnung nicht leicht umkehren, denn aus X = n × P lässt sich n nur schwer ermitteln. Einsatzgebiete der Elliptic Curve Cryptography (ECC) sind ebenfalls Schlüsseltausch (ECCDH) und digitale Signaturen (ECCDSA).

Das wiederholte Addieren auf elliptischen Kurven gilt als besonders gute Einwegfunktion, weil die bekannten Angriffe deutlich aufwendiger sind als bei den herkömmlichen diskreten Logarithmen modulo p. Das erlaubt kürzere Schlüssel.

Für PCs und Notebooks spielt das kaum eine Rolle, sie kommen mit der steigenden Rechenleistung klar, um auch die in Zukunft nötigen längeren Schlüssel zu verwenden. Anders gestaltet sich das bei Geräten mit wenig Performance – Smartcards, Mobiltelefonen – oder Servern, für die das Ver- und Entschlüsseln großer Datenmengen mit hoher Frequenz gefragt ist. Genau dort liegt das Haupteinsatzfeld der elliptischen Kurven. (jab)